Dans mes cours de physique, et en particulier dans le cours Mécanique en Sciences de la nature, il y a 2 enjeux importants:
- les élèves ont dû mal à faire le lien entre les concepts de physique à l’étude et les problèmes qu’ils et elles ont à résoudre
- les élèves n’ont pas les habiletés métacognitives nécessaires pour prendre conscience des défauts de leurs stratégies de résolution de problèmes (ils et elles se satisfont d’une approche par essais et erreurs)
Pour pallier ces problèmes, j’ai créé dans Moodle une banque de questions qui amènent les élèves à conceptualiser correctement des situations-problèmes avant de chercher à manipuler des chiffres dans des équations.
Comprendre des concepts de physique ou manipuler des chiffres à tâtons?
Dans les cours de physique, les élèves doivent apprendre à résoudre des problèmes. Cependant, quand ils et elles travaillent sur des exercices dans un manuel, les élèves arrivent trop souvent à trouver la bonne réponse par essais et erreurs, sans comprendre la physique sous-jacente. Il faut dire que, souvent, la seule rétroaction à leur disposition, c’est la réponse à la fin du livre. Or, avoir la bonne réponse n’implique pas nécessairement de comprendre.
J’ai toujours été conscient de ce problème, mais le déclic qui m’a incité à agir pour y remédier est arrivé lorsque j’enseignais dans une classe d’apprentissage actif. Une équipe d’élèves travaillait sur un problème de dynamique de rotation. De loin, je voyais leur démarche sur leur tableau blanc et je me suis dirigé vers ces élèves confiant qu’ils et elles comprenaient bien. Il n’y avait qu’une petite erreur dans leurs calculs au tableau. Cependant, en discutant avec les élèves pour les aider à repérer leur erreur, j’ai réalisé que, finalement… ils et elles ne comprenaient rien! Ils et elles avaient manipulé des équations, mais ne se représentaient pas du tout la situation décrite dans l’énoncé, et ne savaient pas vraiment ce qu’ils et elles étaient en train de chercher.
Les personnes expertes (que ce soit des enseignants ou des enseignantes ou simplement des élèves avec une attitude experte) ne lisent pas les énoncés des problèmes de la même façon que les élèves qui ont des difficultés.
- Les personnes avec une attitude experte réfléchissent pendant leur lecture. Elles identifient les éléments clés du problème, puis les modèles qui pourraient être utiles pour résoudre le problème (Est-ce un problème de cinématique? Est-ce un problème où le principe de conservation de l’énergie sera utile?). Elles font aussi un schéma de la situation et la représentent graphiquement.
- À l’opposé, les élèves moins habiles se contentent souvent d’identifier les variables et les valeurs numériques qui leur sont associées, puis de chercher dans leur liste une équation dans laquelle les symboles repérés apparaissent. C’est davantage un jeu de sudoku qu’une résolution «réfléchie» d’un problème de physique.
Dans mon cours, je prenais du temps pour poser des questions de «physique conceptuelle» à mes élèves (des questions qui portent sur les concepts étudiés en classe, mais qui n’exigent pas de calculs). Je me disais que de réfléchir à ces questions aiderait les élèves à mieux appliquer les concepts quand viendrait le temps de faire des exercices et de résoudre des problèmes «classiques» impliquant des équations mathématiques. Or, j’ai constaté que la plupart des élèves ne faisaient pas le lien entre les deux.
J’ai donc décidé d’imaginer des situations-problèmes à propos desquelles je poserais d’abord des questions conceptuelles aux élèves, puis une question impliquant un calcul avec des valeurs numériques. Comme tout se rapporte exactement à la même situation, le lien devient si évident que les élèves le perçoivent inévitablement.
J’ai utilisé Moodle pour soumettre mes questions aux élèves. J’utilisais déjà beaucoup Moodle dans mon cours de mécanique depuis la pandémie. J’ai choisi cette plateforme car:
- elle est libre d’accès
- elle est disponible dans la plupart des institutions d’enseignement supérieur
- elle offre la possibilité d’offrir de la rétroaction sous forme de texte, d’équations, d’images et même de vidéos
Déroulement de mon cours
Dans mon cours, j’exploite la pédagogie inversée: les notions de base sont présentées par le biais de vidéos que j’ai déposées sur YouTube et intégrées à Moodle. Sur Moodle, chaque vidéo est accompagnée de questions de compréhension simples (corrigées automatiquement, avec des explications dans la rétroaction), juste pour que l’élève puisse vérifier sa compréhension du contenu de la vidéo.
Puis, en classe, je fais au besoin un bref retour sur certaines notions clés. Ensuite, je pose aux élèves des questions conceptuelles en misant sur l’enseignement par les pairs. Je présente ces questions avec Wooclap, en pigeant dans une banque de questions que mes collègues et moi avons construite ensemble. De temps en temps, je fais aussi des exemples de résolution de problème au tableau, pour montrer aux élèves comment je réfléchis devant un problème à résoudre.
Ensuite, les élèves travaillent en équipe de 3 pour répondre à des questions en plusieurs étapes présentées dans Moodle. (Ce sont les nouvelles questions que j’ai développées pour les aider à faire des liens entre les concepts de physique et l’utilisation des équations mathématiques.) J’essaie toujours de réserver au moins la moitié des heures hebdomadaires du cours théorique à ce travail en équipe.
Exemples de questions dans Moodle
La mise en situation est présentée sans valeurs numériques, mais elle identifie clairement quelles valeurs peuvent être considérées comme connues et lesquelles ne le sont pas.
Voici un exemple simple.
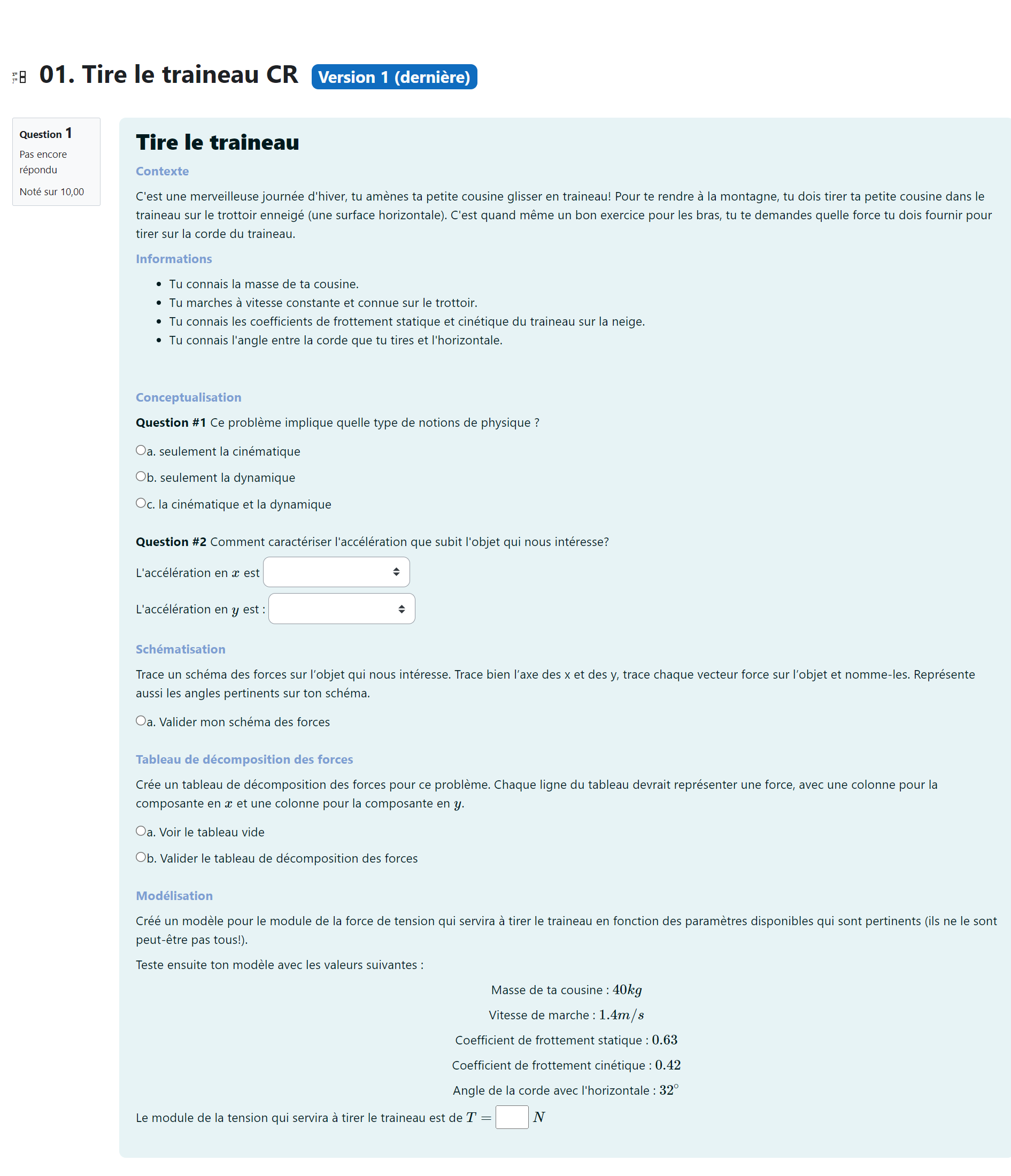
Une mise en situation que j’ai créée dans Moodle pour aider mes élèves à bien comprendre les concepts liés aux problèmes de physique qu’ils et elles résolvent et pour leur montrer à suivre une démarche cohérente.
Dans la Question #1 de l’exemple précédent, les élèves doivent d’abord identifier les notions impliquées dans le problème (ici: la cinématique, la dynamique ou les 2). L’équipe coche la case de son choix puis peut valider sa réponse. C’est un environnement dans lequel il est possible d’apprendre sans pression, puisqu’une mauvaise réponse n’est «jugée» par personne. Le nombre de tentatives permises sur Moodle est illimité. Évidemment, une approche par essais et erreurs est encore possible ici, mais comme le problème est divisé en plusieurs étapes, le raisonnement des élèves est guidé.
Puis, une ou plusieurs autres questions (comme la Question #2 de l’exemple) sont posées aux équipes pour s’assurer qu’elles comprennent la situation-problème. Dans l’exemple ci-dessus, la notion d’accélération est importante. Les équipes sont donc amenées à y réfléchir pour s’assurer qu’elles ont bien analysé la situation.
Ensuite, les équipes sont explicitement invitées à faire un schéma des forces impliquées dans la situation-problème. En cochant la case «Valider mon schéma des forces», les élèves peuvent voir le schéma que j’ai fait moi-même et vérifier que le leur est correct.

Les élèves peuvent voir mon schéma après avoir tracé le leur, pour valider leur réponse.
Puis, les équipes doivent penser à décomposer les forces en jeu dans la situation-problème selon leurs composantes horizontales et verticales.
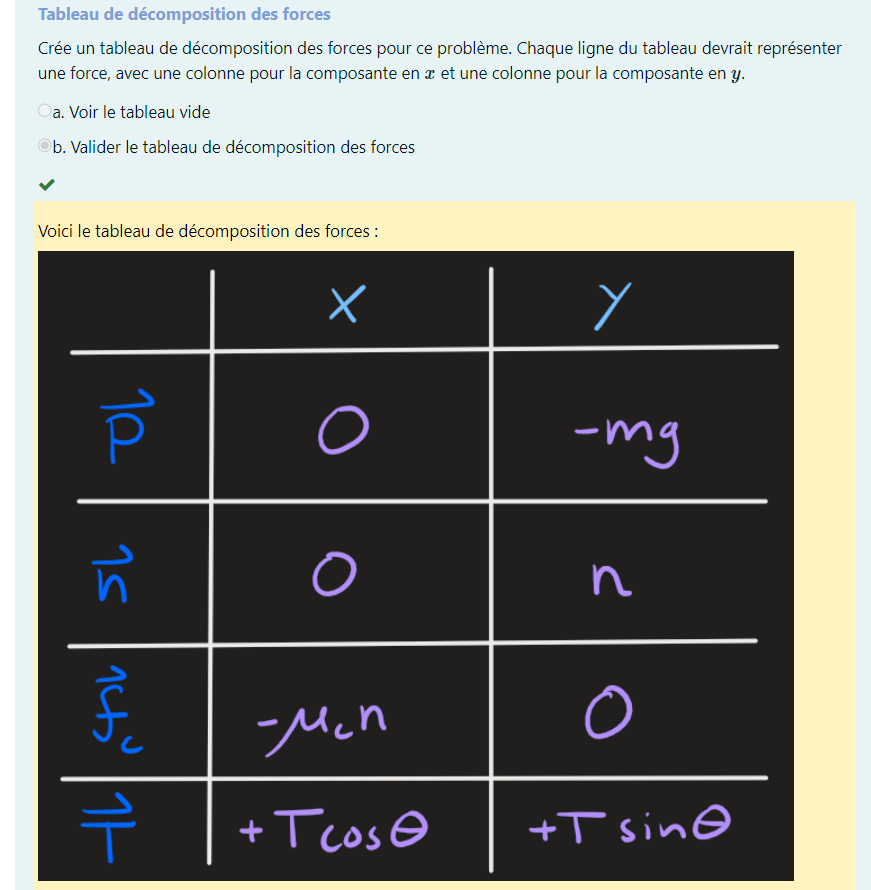
Les élèves peuvent voir ma version du tableau de décomposition des forces pour valider leur réponse.
Après tout cela, les élèves devraient être en mesure d’écrire une équation pour la variable recherchée, qui est dans ce cas-ci la force de tension. À ce stade-ci, ils et elles n’ont aucune valeur numérique à insérer dans leur équation: l’équation obtenue ne contient que les symboles des variables. Cette équation modélise la situation de façon générale. Ensuite, si des valeurs numériques sont fournies, les élèves n’ont qu’à les insérer dans leur équation pour obtenir le résultat très aisément. Pour simplifier la tâche des élèves sur Moodle, je ne leur demande pas de taper leur équation sous forme symbolique. Je leur fournis plutôt des valeurs numériques (qui changent à chaque tentative). De cette façon, les élèves n’ont qu’à entrer une valeur numérique, pour la correction automatique.
Les équipes ne réussissent jamais à répondre à toutes les questions à l’intérieur du temps alloué. Ils et elles doivent poursuivre le travail à la maison.

Un autre exemple de mise en situation dans Moodle
L’évaluation sommative
Chaque semaine, les élèves ont un devoir à faire qui est évalué de façon sommative. Le devoir se fait sur Moodle lui aussi. Il s’agit de 2 ou 3 questions sélectionnées aléatoirement parmi celles réalisées en classe et à la maison. Les questions sont exactement les mêmes que lors du travail en classe, mais sans la modélisation guidée étape par étape. Il n’y a donc que la mise en situation et la question finale avec des valeurs numériques (différentes de celles avec lesquelles les élèves ont travaillé en classe, puisqu’elles changent aléatoirement). Si les élèves avaient bien compris le problème et fait un modèle adéquat en classe (ou à la maison), alors compléter le devoir ne prend que quelques minutes.
Pour moi, ces devoirs sont une façon de motiver les élèves à se tenir à jour dans leur étude (ce qui m’a semblé être un défi pendant la pandémie et juste après). Cependant, la pondération de ces devoirs est faible (environ 10%). Et, surtout, je dis aux élèves que leur note aux examens peut remplacer leur note pour les devoirs, si elle est meilleure. Un étudiant ou une étudiante qui a du mal dans les devoirs, mais apprend au fil du temps et réussit bien l’examen n’est donc pas pénalisé.
Depuis que j’exploite ces questions de modélisation, je pose davantage de questions conceptuelles dans mes examens. Puis, dans les problèmes, je ne fournis plus de valeurs numériques et j’évalue plutôt la capacité des élèves à modéliser correctement les situations. (Dans Moodle, j’ai besoin de mettre les valeurs numériques à la fin pour que la correction automatique fonctionne facilement, mais dans les examens, je corrige moi-même les démarches des élèves.)
Au début de la session, ça prend quelques semaines aux élèves pour comprendre qu’ils et elles doivent vraiment suivre les étapes et modéliser correctement les situations plutôt que de se dépêcher à manipuler les valeurs numériques (qui apparaissent dans le bas des pages sur Moodle dès le début). Les élèves finissent par comprendre que la modélisation algébrique est essentielle pour réussir les devoirs et les examens et cela ne rend pas le cours plus difficile pour autant. Le taux de réussite n’en est pas affecté.
L’importance de diviser les questions en plusieurs étapes
Quand j’ai commencé à utiliser cette approche, je n’avais pas découpé mes questions en plusieurs étapes sur Moodle (je ne demandais pas d’identifier les notions pertinentes, de faire un schéma, etc.). Cela ne suffisait pas pour atteindre mes objectifs, puisque plusieurs élèves ont tout simplement décalé leur approche de tâtonnement: plutôt que de faire des essais et erreurs avec des valeurs numériques, les élèves le faisaient avec les symboles algébriques pour obtenir le modèle.

